Deeper Scrutiny of Mathematical Systems Through Hofstadter’s (1979) Gödel, Escher, Bach: An Eternal Golden Braid.

After my previous blog regarding Set Theory and Russell’s Paradox, I was recommended this Hofstadter book by one of my Twitter connections, Washington State University professor @PezeshkiCharles. Many themes are explained, especially the book’s central themes of self-reference and recursion in mathematical truisms. I decided to read it, and it is a behemoth of a book, not necessarily the length, but the density of it. I plan to have this blog finished around 2500 words and there are so many concepts presented that this doesn’t even do it justice. All 777, or 800 depending on the version, pages offer deep and dense concepts that require further reflection and understanding – multiple readings are needed. First thumb through, I was able to get a sense of what the overall book is about – with some help from review articles related. What I hope to provide is somewhat of a brief synopsis, concepts that are interesting and related to my previous writings, scrutiny of the work, and a sort of ‘literary analysis’ of the deeper meanings I see in the book.

Brief Synopsis

Gödel, Escher, Bach: An Eternal Golden Braid (often abbreviated as GEB) is a book written by Douglas Hofstadter in 1979. It explores various interconnected themes from mathematics, music, and art while delving into cognitive science and artificial intelligence. The book’s title refers to three influential figures in their respective fields: the mathematician Kurt Gödel, the artist M.C. Escher, and the composer Johann Sebastian Bach.

Hofstadter’s central idea in GEB is to explore the concept of self-reference and its implications in different domains. He uses Gödel’s incompleteness theorems as a starting point to discuss the limitations of formal systems and the inherent paradoxes that arise within them. Gödel’s theorems showed that no consistent formalized system can prove all true statements about numbers within that system. Hofstadter extends this idea to other domains, such as art and music, suggesting that self-reference and recursive patterns are fundamental to creative expression.

Gödel’s Incompleteness Theorem and Set Theory

One concept that the book focuses on is Gödel’s incompleteness theorem and how it impacts the mathematical world. Gödel’s incompleteness theorem, formulated in 1931, states that within any consistent formal system that is powerful enough to express arithmetic, there exist true statements that cannot be proven within that system. In other words, no matter how rich and comprehensive a formal system may be, it will always have inherent limitations with certain statements remaining undecidable. What we have here are three rules related to the theorem:

1. Every mathematical system has untrue statements that cannot be proven within the system.
2. Every formula has an error.
3. Within infinite sets, there is always a contradiction.

The first incompleteness theorem states that within any consistent formal system, you have arithmetic and truth statements. In summation, every supposed true statement may not be true, and every false statement may not be false. I don’t necessarily agree with this – well, I agree this fits with the original Set Theory, but Hofstadter only mentions formal or propositional logic briefly without expanding on how Gödel’s process has some issues addressing propositional logic. First, he explains that a machine with the ability to have inputs is not running on a formal logic system; however, it is exactly what a formal logic system is, propositional inputs for machines based on a binary arrangement. Second, an understanding of propositional calculus (basic propositions and logical connectives to make axioms) leading to a concept of fantasies within fantasies, loosely based on Chisholm’s Many Worlds Interpretation (MWI), is still contained within an axiomatic system.

One might say that with the advancement of axiomatic principles in math since the book’s publication in 1979 – is Gödel’s incompleteness theorem, ironically, incomplete?

Gödel’s theorem relies on certain assumptions, such as the assumption of consistency and the ability to express arithmetic within a formal system. I, with many others, argue that these assumptions might not hold universally, limiting the generalizability of the theorem and its applicability to other domains. Although Gödel’s theorem reveals limitations in formal systems, it does not provide concrete guidance on how to address these limitations or construct alternative systems. I feel this can be solved by understanding propositions building to axioms, then axioms building to truth claims.

These axiomatic systems construct further comprehensive and powerful formal systems by augmenting the set of axioms or introducing additional rules of inference – challenging Gödel’s theorem. If we are to understand the process of truth, coming from arguments about truth, then formal logic provides a systematic framework for reasoning and evaluating the validity of arguments based on well-defined rules of inference. It is concerned with the consistency and soundness of formal systems, ensuring that conclusions derived from valid reasoning preserve truth. Gödel’s incompleteness theorem focuses on the limitations of formal systems – proving all true statements within themselves in failing to expand the axiomatic system.

If we are to say that the incompleteness theorem suggests that things can’t be proven true or false, of what use is the theorem to be applied to claim the entire book’s existence? Are we not to test Gödel’s incompleteness theorem to justify its use in our world? How did Gödel’s incompleteness theorem form without an assessment of true and false? Is it true that Escher’s lithographs are art on 2D print, describing a paradoxical image of two hands drawing each other into existence? Yes, of course, it is true, it is known artwork. Can you reach into the painting and shake Escher’s infamous hands? No, that is a false statement and can be explained through different forms of logical notation.

This is not to denigrate Gödel’s incompleteness theorem, and its use for challenging Set Theory is warranted but still feels incomplete when discussing the entire body of axiomatic principles and propositional logic.

Understanding The Exemplum Magnum (or the Large Pattern)

This book does a fantastic job of understanding patterns in different domains and how they make sense within a mathematical realm. One example of this is Hofstadter’s concept of strange loops found within the works of all three subjects.

“The ‘Strange Loop’ phenomenon occurs whenever, by moving upwards (or downwards) through the levels of some hierarchical system, we unexpectedly find ourselves right back where we started.” (p. 18)

“The lithograph Ascending and Descending (Fig. 6), in which monks trudge forever in loops, is the loosest version since it involves so many steps before the starting point is regained.” (p. 21)

This introduces the concept of higher-level loops and lower-level loops. Higher-level loops refer to self-referential systems that involve the concept of “I” or self-awareness. These loops give rise to consciousness and a sense of personal identity. They are complex, introspective processes that enable us to reflect upon our thoughts and experiences. On the other hand, lower-level loops are recursive patterns and structures that operate at a more fundamental level. They involve repetitive processes that generate intricate and often unexpected behavior. Lower-level loops are the building blocks of higher-level loops and contribute to the emergence of complexity and creativity in various domains, such as art, music, and cognition.

There is also the concept of Escher’s understanding that he is an ‘invisible force’ on the drawing hands as he is the unseen factor in the equation; as in, he is the one creating the hands who create themselves into existence through the lithograph as per Figure 135 in GEB (see image below). Keep this in mind as we discuss infinity in the proceeding section.

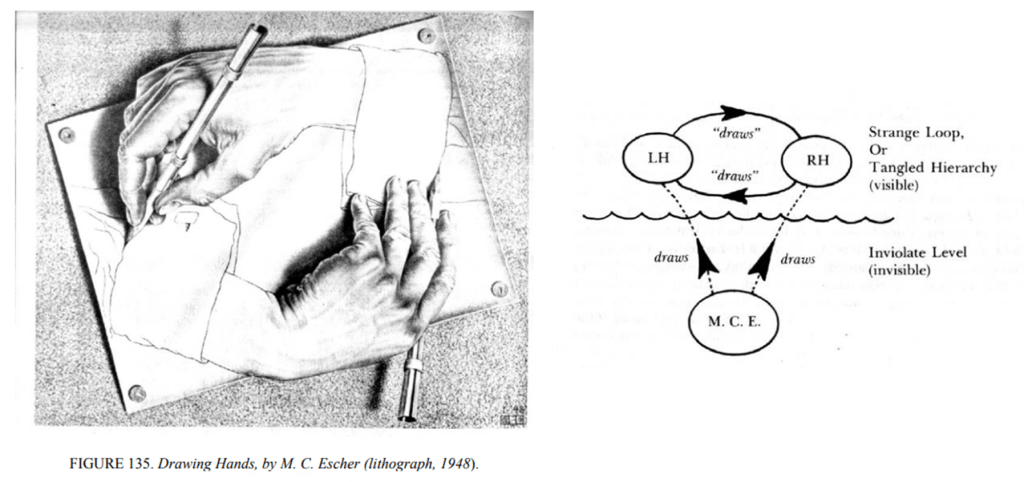
This large pattern can be described as a Gödel Vortex – we can call it Gödel’s Vortex – where the tangled hierarchy of systems discussed in the book intersects to create a pattern toward complete self-knowledge or self-ignorance. The vortex is a metaphorical representation of the self-referential loops of ideas that arise when considering Gödel’s incompleteness theorem and related concepts. It represents the swirling and recursive nature of thoughts that arise when contemplating the profound implications of Gödel’s theorem on mathematics, formal systems, and consciousness.

“Now if some outside agent suggests ‘L’ as the next choice to the robot, the suggestion will be picked up and channeled into the swirling mass of interacting symbols. There, it will be sucked inexorably into interaction with the self-symbol, like a rowboat being pulled into a whirlpool. That is the vortex of the system, where all levels cross. Here, the ‘L’ encounters a Tangled Hierarchy of symbols and is passed up and down the levels. The self-symbol is incapable of monitoring all its internal processes, and so when the actual decision emerges-‘L’ or ‘R’ or something outside the system-the system will not be able to say where it came from… From this balance between self-knowledge and self-ignorance comes the feeling of free will.” (p. 708)

This continual self-referential pattern that the human condition finds itself in is quite illuminating. One could see the process of science itself as a constant infinite loop of things known and things waiting to be known. A continual loop of knowledge acquisition and knowledge attainment – is really at the heart of the concept of humans as they learn from birth to death. Our existential understanding is inexorably tied to this ‘loop vortex’ in some way – even if it is theoretical.

What Is Infinity…Really?

The word infinity has been a mainstay in our lexicon; made popular by the Pixar movie, Toy Story, where the character Buzz Lightyear says the quote “To infinity…and beyond!” Never mind about the inherent contradiction of that phrase, it’s a kid’s movie after all. But it leads to the question, what is infinity? What does this simple sign (∞) mean? It has been a question since at least Greek Antiquity with Aristotle questioning concepts of potential infinite and actual infinite.

Potential infinite refers to a process or sequence that can continue indefinitely without ever reaching a definite endpoint. It is an indefinite, unbounded progression that can be extended indefinitely. For example, the counting numbers (1, 2, 3, 4, and so on) represent a potential infinite because you can keep counting without ever reaching a final number. On the other hand, an actual infinite refers to a collection or set that contains an infinite number of elements. It is a completed, fully formed infinite set. For example, the set of all integers (…, -3, -2, -1, 0, 1, 2, 3, …) represents an actual infinite because it encompasses an infinite number of integers.

Although Gödel’s Vortex is purely a metaphorical concept from Hofstadter, it provides an interesting understanding of infinity and its recursive and self-referential nature. However, there is a deeper question to be asked here. Say you are one of the monks in Escher’s drawing walking up a never-ending staircase, this is your infinite knowledge that is known, but what about unknown infinite knowledge, or yet to be discovered? Obviously, the image is an optical illusion to teach us about relativity, but let’s go with the stairs being truth within our world. For example, the staircase is situated on a roof with a foundation holding it up. Perhaps what Escher is saying is that our referential dimensions of infinity are held to the standard of the stairs, but what about extra-dimensional understanding? If the staircase is actualized and a form of ‘in-being’ it’s not nothing. Therefore, if we accept that known knowledge is built from previously known knowledge, there is previously known knowledge on how to build the steps.

Here is my assessment. The concept of the infinite – related to Aristotle – can be seen as a first-dimension infinite as the potential and actual infinities are on a single plane of existence. Our concept of the infinite – as in what we develop – is a two-dimensional infinite which is a plane that extends in all directions. What we see and conceptualize as humans – such as Escher’s drawings or Bach’s harmonic labyrinth – is a three-dimensional infinite which allows for the existence of infinite spatial arrangements. For instance, we can envision infinite variations of objects and structures in three-dimensional space. Moreover, the concept of an infinite universe or an infinite expanse of space relates to the idea of an actual infinite.

But there is one more infinite that extends beyond the GEB concepts, and anything that we have discovered yet (the unknown infinite knowledge if you will). The four-dimensional infinite, representing time, implies that events and moments can continue indefinitely into the past and future without any definitive endpoint. Who started the staircase? Who started the labyrinth? Figure 135 in the book provides a brief concept of this, as Escher himself acts as a fourth-dimensional being in his two-dimensional lithograph. In this never-ending staircase, or two hands coming into existence, when did it all start? True infinity must encompass a fourth-dimensional understanding to be a true infinity.

***

As always, I will look more into this as it is something I feel has important epistemological implications. I do welcome other people to look into this further and provide insight. Discussions like this have been happening for centuries, but more discussion needs to happen on defining a new form of true infinity based on dimensional understanding. Perhaps something for a future blog.

P.S. read Chuck’s blog at https://empathy.guru/. He has some great stuff on there that is quite insightful.